Wavelets on Domains and Surfaces
Wavelet discretizations of boundary value problems
exhibit several advantages, like well-conditioning,
compressibility, or adaptivity. Particularly our
wavelet Galerkin scheme solves boundary integral
equations in linear complexity. To that end, wavelet
bases are required which provide sufficiently many
vanishing moments. Our realization is based on biorthogonal
spline wavelets derived from the multiresolution developed
by Cohen, Daubechies and Feauveau.
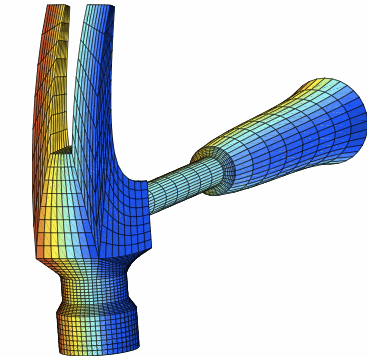
Parametric surface representations with mesh on level 3
The domain or surface is subdivided into smooth
four-sided patches which are images of the unit square
under smooth diffeomorphisms. Such parametric
surface representations can directly be obtained from
computer aided design (CAD) and are recently studied
in the context of isogeometric analysis. The wavelets
are constructed by lifting wavelets from the unit
square to the surface via parametrization.
Gluing across the patch boundaries yields
globally continuous wavelet bases.

| |
|
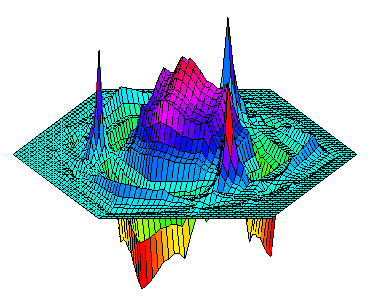
primal scaling function at a degenerated vertex
| |
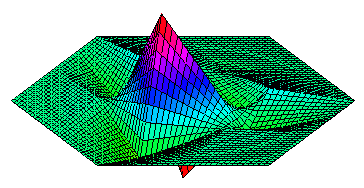
dual scaling function at a degenerated vertex
|
| |
|
|
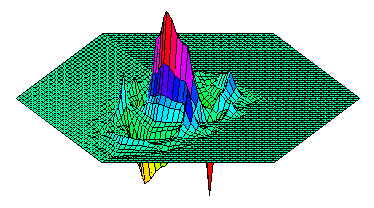
primal wavelet near an interface
| |
dual wavelet near an interface
|
Selected Publications
-
H. Harbrecht and R. Schneider.
Biorthogonal wavelet bases for the boundary element method.
Math. Nachr., 269-270:167-188, 2004.
-
H. Harbrecht and R. Stevenson.
Wavelets with patchwise cancellation properties.
Math. Comput., 75(256):1871-1889, 2006.
-
H. Harbrecht and M. Randrianarivony.
From Computer Aided Design to Wavelet BEM.
Comput. Vis. Sci., 13(2):69-82, 2010.