Wavelet Galerkin Schemes for Nonlocal Operators
Various problems in science and engineering can be formulated as boundary integral equations. These are numerically solved by the boundary element method. For example, the boundary element method is the favourable approach for the treatment of exterior boundary value problems, in particular for problems in electromagnetism or in case of the Helmholtz equation. Nevertheless, traditional discretizations will lead in general to very large linear systems with densely populated and possibly ill-conditioned matrices. This makes the computation very costly in both respects, the computation time and computer memory requirements.
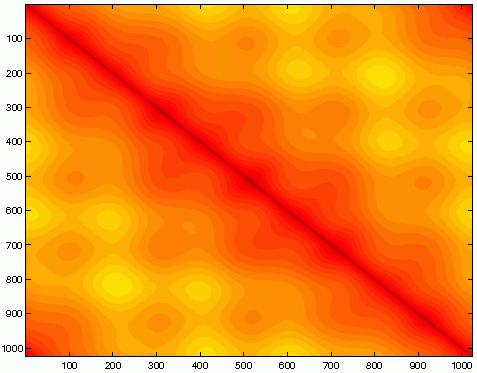
|
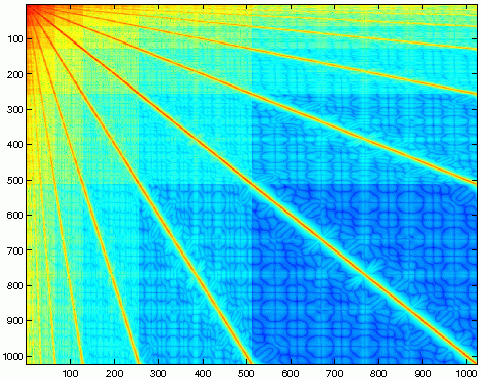
| |
| traditional discretization | wavelet discretization |
A Galerkin discretization with wavelet bases results in quasi-sparse matrices. In fact, the system matrix becomes finger band structured in wavelet coordinates. Discarding the nonrelevant matrix entries is called matrix compression. The sparsity pattern is chosen carefully by a level dependent compression strategy such that the optimal order of convergence of the Galerkin scheme is not violated.
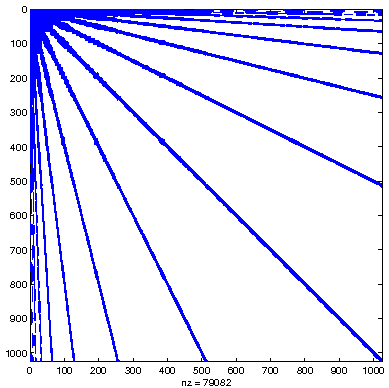
compression pattern
The compressed matrix is assembled by applying an exponentially convergent hp-quadrature method. A diagonal scaling yields a well-conditioned linear system of equations. Our approach is proven to solve boundary integral equations with linear complexity by preserving the optimal order of convergence of the underlying Galerkin scheme.
Selected Publications
-
W. Dahmen, H. Harbrecht, and R. Schneider.
Compression techniques for boundary integral equations.
Asymptotically optimal complexity estimates.
SIAM J. Numer. Anal., 43(6):2251-2271, 2006.
-
H. Harbrecht and R. Schneider.
Wavelet Galerkin schemes for boundary integral
equations. Implementation and quadrature.
SIAM J. Sci. Comput., 27(4):1347-1370, 2006.
-
H. Harbrecht and R. Schneider.
Rapid solution of boundary integral equations by wavelet Galerkin schemes.
In R. DeVore and A. Kunoth, editors,
Multiscale, Nonlinear and Adaptive Approximation, pages 249-294.
Springer, Berlin-Heidelberg, 2009.

