Wavelet BEM on Molecular Surfaces
Continuum solvation models are widely used to model quantum effects of molecules in liquid solutions. Our research focuses on the polarizable continuum model (PCM). In this model, the molecule under study (the solute) is located inside a cavity \(\Omega\), surrounded by a homogeneous dielectric (the solvent). The solute-solvent interactions between the charge distributions which compose the solute and the dielectric are reduced to those of electrostatic origin.The interface between the solute and the solvent constitutes the molecule's surface. In general, the molecule \(\Omega\) is defined as a union of balls, centered in the nuclei positions and of radii related to the van der Waals radius. The resulting surface is called the van der Waals surface (VWS). Whereas, the solvent accessible surface (SAS) coincides with the VWS surface except for scaling of the radii. Another class of surfaces are solvent excluding surfaces (SES), also known as Connolly surfaces. They are defined from the VWS model by rolling a spherical probe over the surface.

|
| |
| Van der Waals surface of benzene | Connolly surface of benzene |
According to classical electrostatics, the charge distribution of the solute, inside the molecule, polarizes the dielectric continuum, which in turn polarizes the solute's charge distribution. This interaction might be expressed in terms of an apparent surface charge (ASC) which resides on the molecule's surface. This is known as the ASC approach. The underlying electrostatic problem is described by a transmission problem for the Laplacian in the whole space \(\mathbb{R}^3\). Therefore, the integral equation formalism (IEF) offers a favourable approach to compute the electrostatic solute-solvent interaction.
Boundary integral equations are generally solved by the boundary element method (BEM). BEM is a well established tool in PCM. However, traditional discretizations lead to densely populated and possibly ill-conditioned system matrices. Both features pose serious obstructions to the efficient numerical treatment of such problems. Modern methods for the rapid BEM solution reduce the complexity to almost or even optimal rates. We apply the wavelet Galerkin scheme which produces the approximate solution with discretization error accuracy in linear complexity. The present research is a joint project with Luca Frediani (University of Tromsø, Norway).

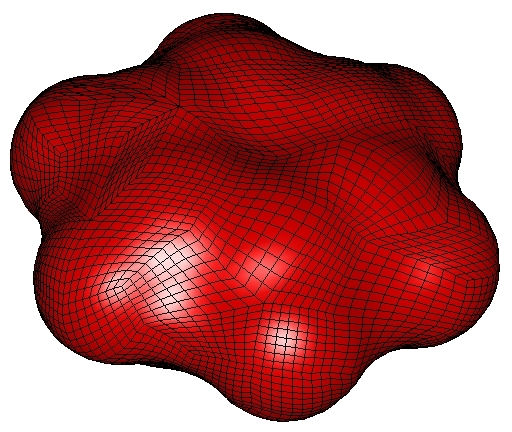
Parametrization of the SES surface of an ice cluster
Selected Publications
-
H. Harbrecht and M. Randrianarivony.
Wavelet BEM on molecular surfaces. Parametrization and implementation.
Computing,
86(1):1-22, 2009.
-
W. Weijo, M. Randrianarivony, H. Harbrecht, and L. Frediani.
Wavelet formulation of the polarizable continuum model.
J. Comput. Chem., 31(7):1469-1477, 2010.
-
H. Harbrecht and M. Randrianarivony.
Wavelet BEM on molecular surfaces. Solvent excluded surfaces.
Computing,
92(4):335-364, 2011.
-
M. Bugeanu, R. Di Remigio, K. Mozgawa, S. Reine, H. Harbrecht, and L. Frediani.
Wavelet formulation of the polarizable continuum model. II. Use of piecewise bilinear boundary elements.
Phys. Chem. Chem. Phys., 17:31566-31581, 2015.

