FEM for Elliptic Problems with Random Input Data

In recent years it has become more and more important to model and simulate boundary value problems with random input parameters. If a statistical description of the input data is available, one can mathematically describe data and solutions as random fields and aim at the computation of corresponding deterministic statistics of the unknown random solution. Applications are, besides traditional engineering, for example biomedical or biomechanical processes. To simulate biomechanical processes one has, on the one hand, uncertain domains arising from e.g. tomographic data. On the other hand, one often has only estimates on the material parameters.

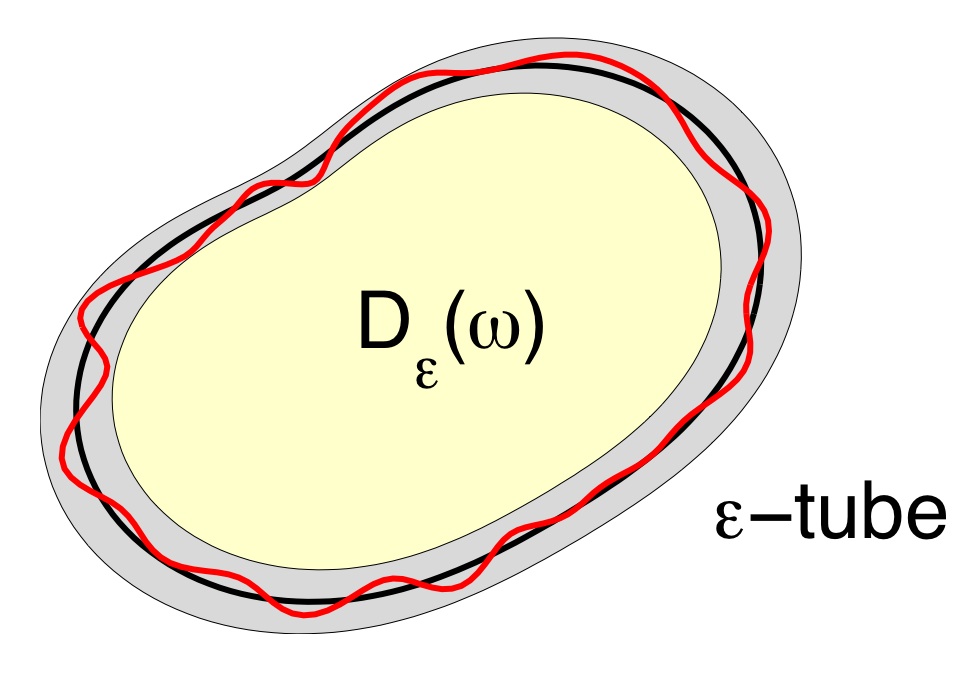
Uncertainty might stem from the loading, the coefficients of the differential operator, or the domain $ D$ of definition. In case of random loadings, the random solution depends linearly on the random input data. But this is not valid any more if the differential operator’s coefficients or the domain of definition are random. Nevertheless, assuming small random perturbations around a nominal input parameter, we can linearize in order to approximate the solution's nonlinear dependence on this parameter. That way, we are also able to treat boundary value problems on random domains or with random diffusion matrix.



The random domain is a perturbation of the nominal domain $ D$


From statistical information of the random input data, we like to compute statistics of engineering interest for the random solution of the boundary value problem. In particular, we like to compute the expectation

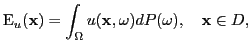
$\displaystyle \operatorname{E}_u({\bf x}) = \int_{\Omega} u({\bf x},\omega) dP(\omega),\quad {\bf x}\in D, $

and the two-point correlation

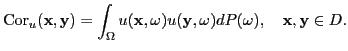
$\displaystyle \operatorname{Cor}_u({\bf x},{\bf y}) = \int_{\Omega} u({\bf x},\omega) u({\bf y},\omega) dP(\omega), \quad {\bf x},{\bf y}\in D. $

From these quantities the variance is derived by

$\displaystyle \operatorname{Var}_u({\bf x}) = \operatorname{Cor}_u({\bf x},{\bf x}) -\operatorname{E}_u^2({\bf x}). $

Our goal of computation is thus as follows: for given mean and two-point correlation of the stochastic input parameter, compute, to leading order, the mean and the two-point correlation of the random solution of the boundary value problem.

The $ p$-th stochastic moment satisfies a boundary value problem with the $ p$-fold tensor product of the underlying elliptic operator $ A\otimes A\otimes \dots\otimes A$ on the $ p$-fold tensor product domain $ D\times D\times\cdots\times D$. Therefore, the two-point correlation is given by a partial differential equation on the tensor product domain $ D\times D$. We employ a sparse tensor product approximation to solve this high dimensional problem efficiently. Especially, we are going to use the combination technique or multilevel frames instead of wavelet or multilevel bases to approximate the functions from the sparse tensor product space. Thus, we can use standard multigrid hierarchies and traditional finite elements.



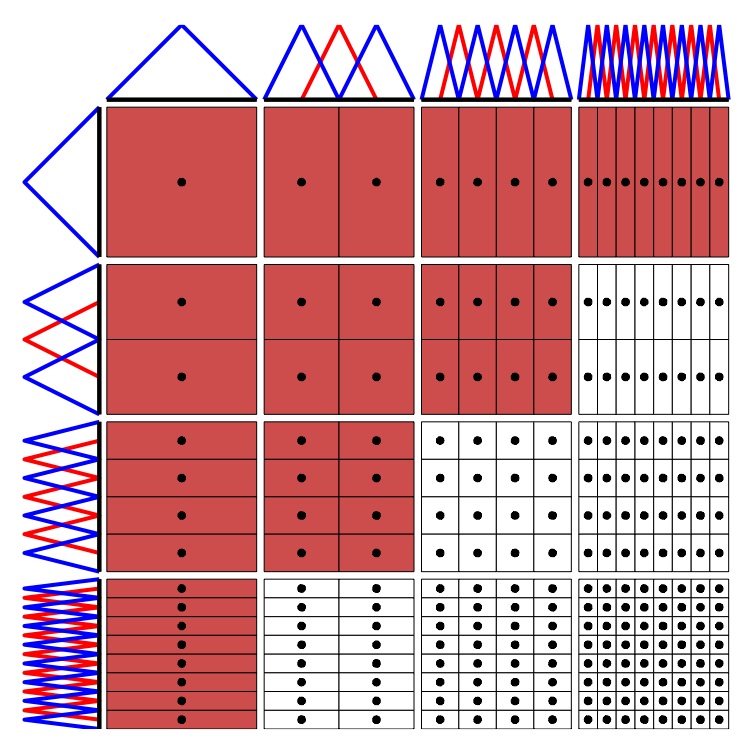
Wavelet or multilevel basis and multilevel frame

Selected Publications

  1. H. Harbrecht, R. Schneider, and C. Schwab. Sparse second moment analysis for elliptic problems in stochastic domains. Numer. Math., 109(3):385-414, 2008.

  2. H. Harbrecht, R. Schneider, and C. Schwab. Multilevel frames for sparse tensor product spaces. Numer. Math., 110(2):199-220, 2008.

  3. H. Harbrecht. On output functionals of boundary value problems on stochastic domains. Math. Methods Appl. Sci., 33(1):91-102, 2010.

  4. H. Harbrecht. Second moment analysis for Robin boundary value problems on random domains. In M. Griebel, editor, Singular Phenomena and Scaling in Mathematical Models, pages 361-382, Springer, Berlin, 2013.

  5. H. Harbrecht, M. Peters, and M. Siebenmorgen. Combination technique based k-th moment analysis of elliptic problems with random diffusion. J. Comput. Phys., 252:128-141, 2013.

Support

This research has been supported by the SNF-project Rapid solution of boundary value problems on stochastic domains.