Inverse Obstacle Scattering
It is well known that the propagation of an acoustic wave in a homogeneous, isotropic, and inviscid fluid is approximately described by a velocity potential \(U({\bf x},t)\) satisfying the wave equation \(U_{tt} = c^2\Delta U\). Here, \(c\) denotes the speed of sound, \(v = U_{\bf x}\) is the velocity field, and \(p = -U_t\)is the pressure. If \(U\) is time harmonic, that is \(U({\bf x},t) = \operatorname{Re}\big(u({\bf x})e^{-i\omega t}\big)\), \(\omega>0\), in complex notation, then the complex-valued space-dependent \(u\) satisfies the Helmholtz equation \[ \Delta u + \kappa^2 u = 0\quad\text{in}\ \mathbb{R}^3\setminus\overline{\Omega}. \] The domain \(\Omega\subset\mathbb{R}^3\) describes an obstacle and \(\kappa = \omega/c\) is the wave number. We assume that \(\Omega\) is simply connected and bounded with smooth boundary \(\Gamma = \partial\Omega\). For sound-soft obstacles, the pressure \(p\) vanishes on \(\Gamma\), which leads to the Dirichlet boundary condition \[ u=0\quad\text{on}\ \Gamma. \]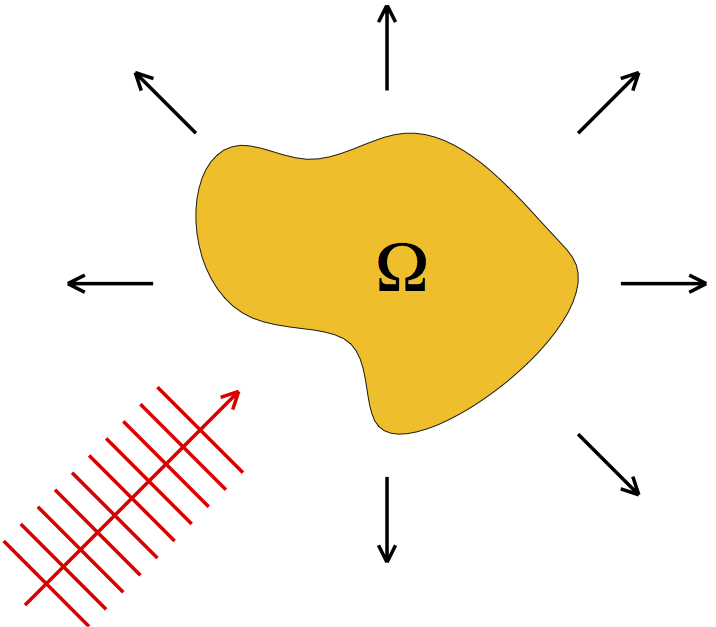
We shall consider the situation that \(u = u_i+u_s\) is composed of a known incident plane wave \(u_i({\bf x}) = e^{i\kappa {\bf d}\cdot{\bf x}}\) with direction \({\bf d}\), and a scattered wave \(u_s\). The scattered field satisfies the Sommerfeld radiation condition \[ \lim_{r\to\infty} r \left\{ \frac{\partial u_s}{\partial r} - i\kappa u_s\right\} = 0,\quad r = \|{\bf x}\|, \] which implies the asymptotic behaviour \[ u_s({\bf x}) = \frac{e^{i\kappa\|{\bf x}\|}}{\|{\bf x}\|} \left\{u_\infty\bigg(\frac{\bf x}{\|{\bf x}\|}\bigg) + \mathcal{O}\bigg(\frac{1}{\|{\bf x}\|}\bigg)\right\}, \quad \|{\bf x}\|\to\infty. \] The function \(u_\infty:\mathbb{S}^2 :=\{{\bf x}: \|{\bf x}\|=1\}\to\mathbb{C}\) is called the far-field pattern.
The inverse obstacle scattering problem reads as follows: Given the direction \({\bf d}\), the far field pattern \(u_\infty\) of the scattered wave, find the domain \(\Omega\). In cooperation with Thorsten Hohage (Georg-August-University of Göttingen, Germany), we are developing efficient methods to solve this severely ill-posed inverse problem. Generating for example synthetic data from the following dolphin
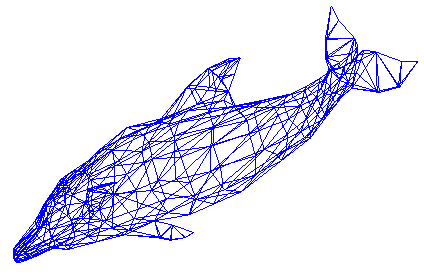
we gain the reconstruction

Selected Publications
-
H. Harbrecht and T. Hohage.
Fast methods for three-dimensional inverse obstacle scattering.
J. Integral Equations Appl., 19(3):237-260, 2007.
-
H. Harbrecht and T. Hohage.
A Newton method for reconstructing non star-shaped domains in
electrical impedance tomography.
Inverse Probl. Imaging, 3(2):353-371, 2009.

